Estadística: com introduir-la a través de preguntes i respostes

Descobreix la proposta de Math Bits per introduir l’estadística a l’ESO i coneix en què consisteix el projecte SALMO.

24 de enero de 2025

Al començament de l’educació secundària, l’estadística pot semblar una disciplina principalment descriptiva. En efecte, les tècniques de l’estadística inferencial no s’introdueixen formalment fins als cursos posteriors. Malgrat això, és imprescindible plantejar i donar resposta a preguntes a partir de les dades, des del principi. Per exemple, en un projecte que tingui com a objectiu esbrinar si els salmons salvatges són diferents dels de piscifactoria, es pot calcular la mitjana d’una característica mesurable en dues mostres, una de cada tipus de salmó. Si els valors obtinguts són molt diferents, aleshores es pot concloure que, efectivament, sembla haver-hi una diferència en aquest sentit, sense entrar en quantificar la significativitat estadística de la diferència.

Com veurem, aquest projecte sobre salmons permet articular diferents idees i conceptes d’estadística en aquesta unitat de Math Bits.

El projecte SALMO

A la primera lliçó «Explorem», es presenta el projecte i es porta a terme la recollida de dades. Aquí l’alumnat ha de prendre decisions sobre els trets a considerar. Alguns d’aquests trets o característiques poden ser quantitats de magnitud mesurables, com la massa o la longitud, mentre que d’altres no, com la forma de la boca o el color. D’aquesta manera, l’activitat posa sobre la taula la distinció entre variables quantitatives (contínues o discretes) i variables qualitatives (ordinals o nominals). En aquesta activitat, s’aborda també la diferència entre individu, mostra i població.

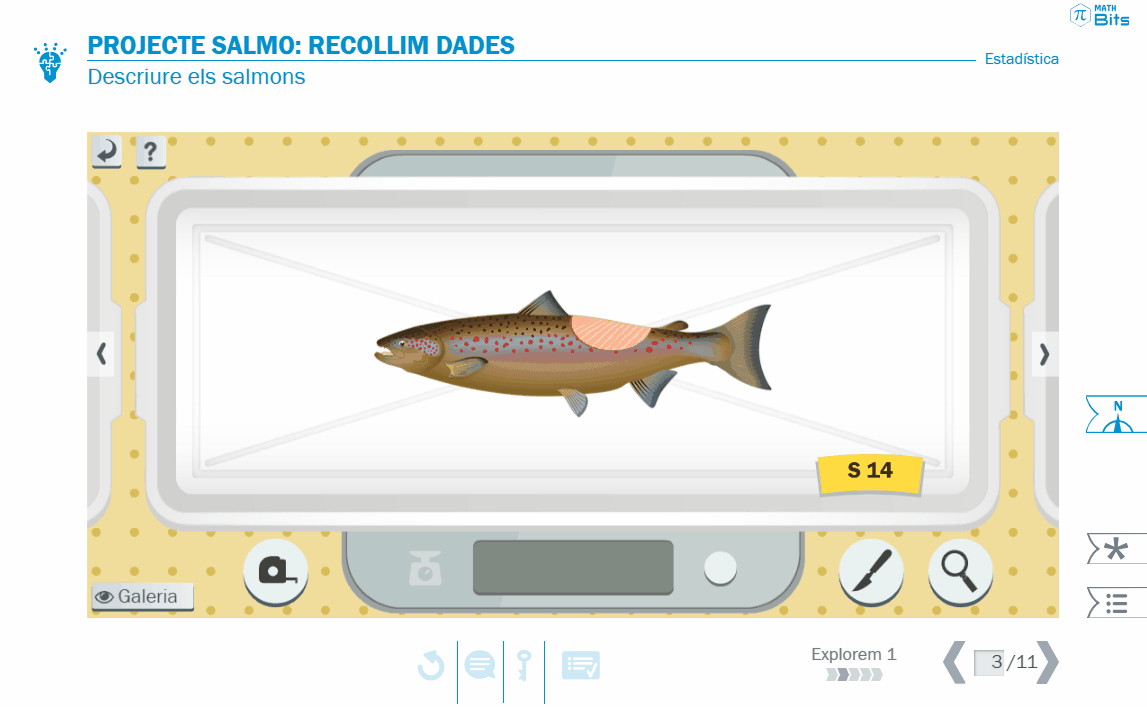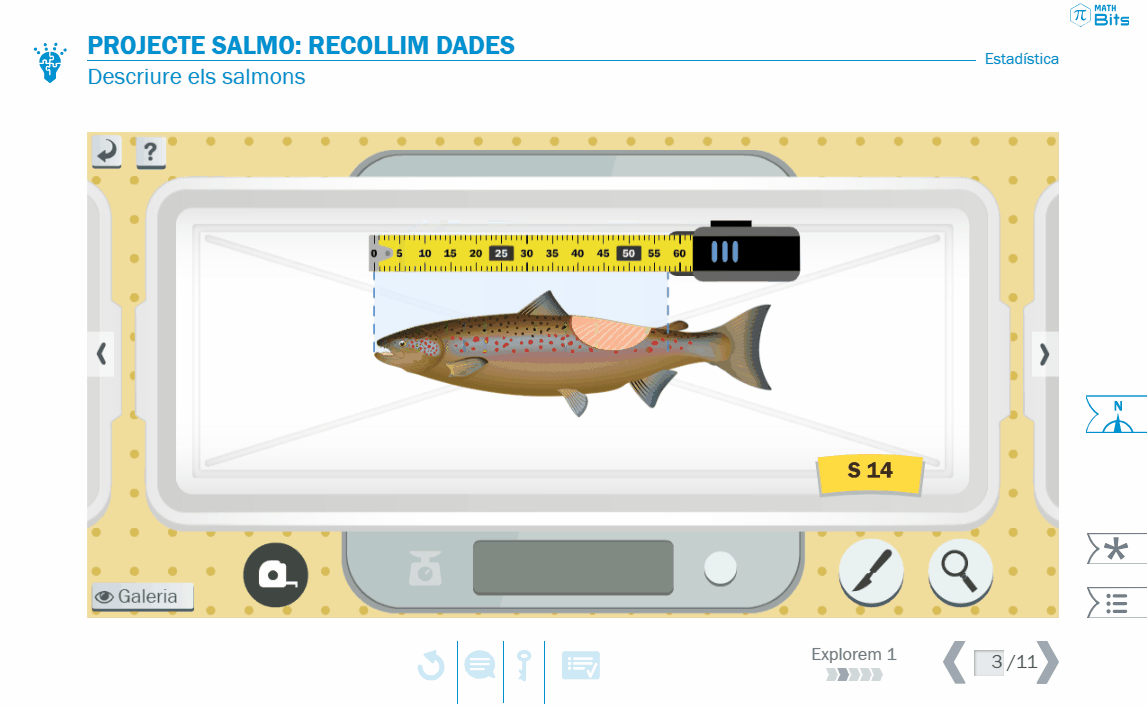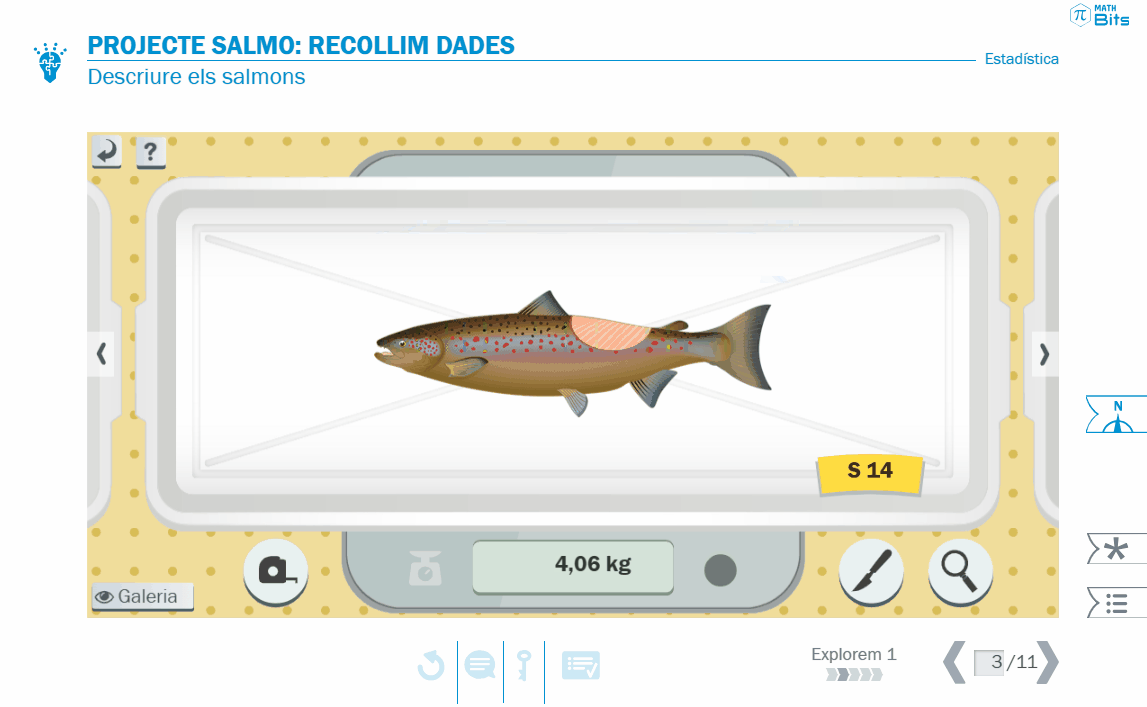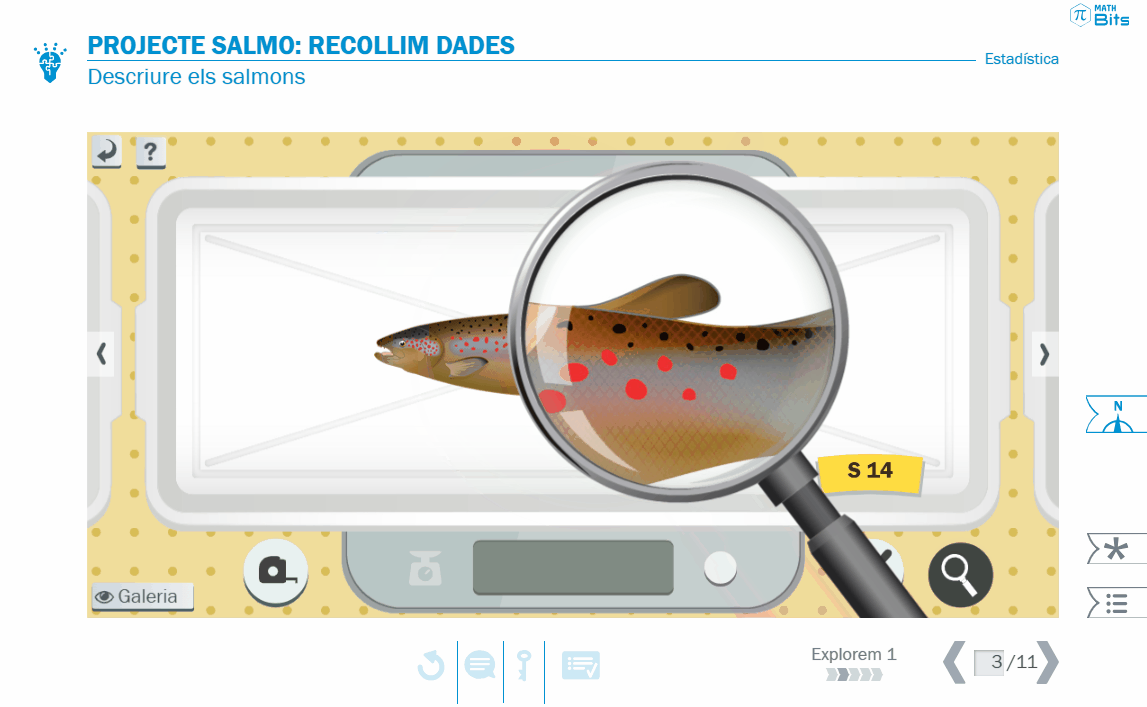
Recollida de dades al projecte SALMO.

Organització de les dades: les taules de freqüències

Mitjançant el seguiment de les fases d’un projecte estadístic, a continuació es planteja una situació d’exploració en la qual s’ha d’organitzar la informació, fent ús de les taules de freqüències. Així, s’introdueix la distinció entre freqüència absoluta i freqüència relativa. La freqüència absoluta es presenta com una forma de sistematitzar els recomptes. En canvi, la freqüència relativa s’introdueix a partir de la necessitat de comparar mostres o poblacions de mida desconeguda.

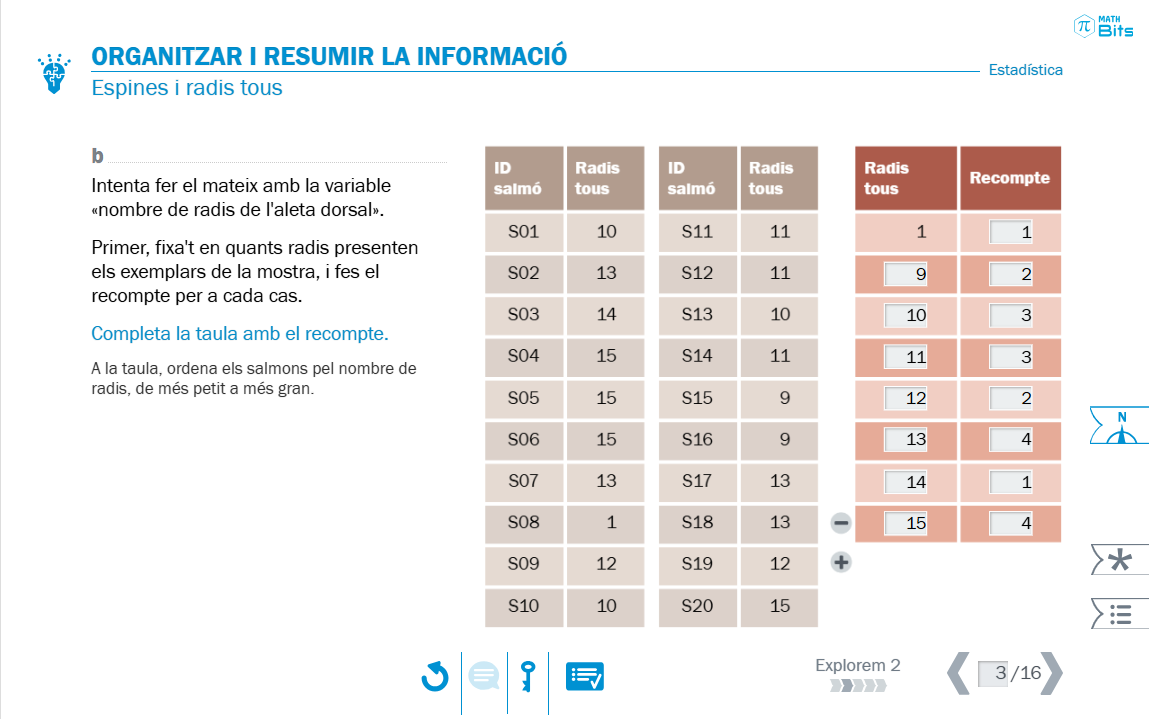
Recurs interactiu inicial per construir les taules de freqüència des del recompte.

Elaborar taules de freqüència implica una pèrdua parcial d’informació. En particular, si s’analitza una variable contínua que s’agrupa per intervals, la taula de freqüència a partir de les marques de classe no permet recuperar la informació dels valors originals. D’altra banda, si la variable és discreta o qualitativa sí que podem recuperar les dades «en brut», tot i que s’hagi perdut l’ordre en què van ser recollides.

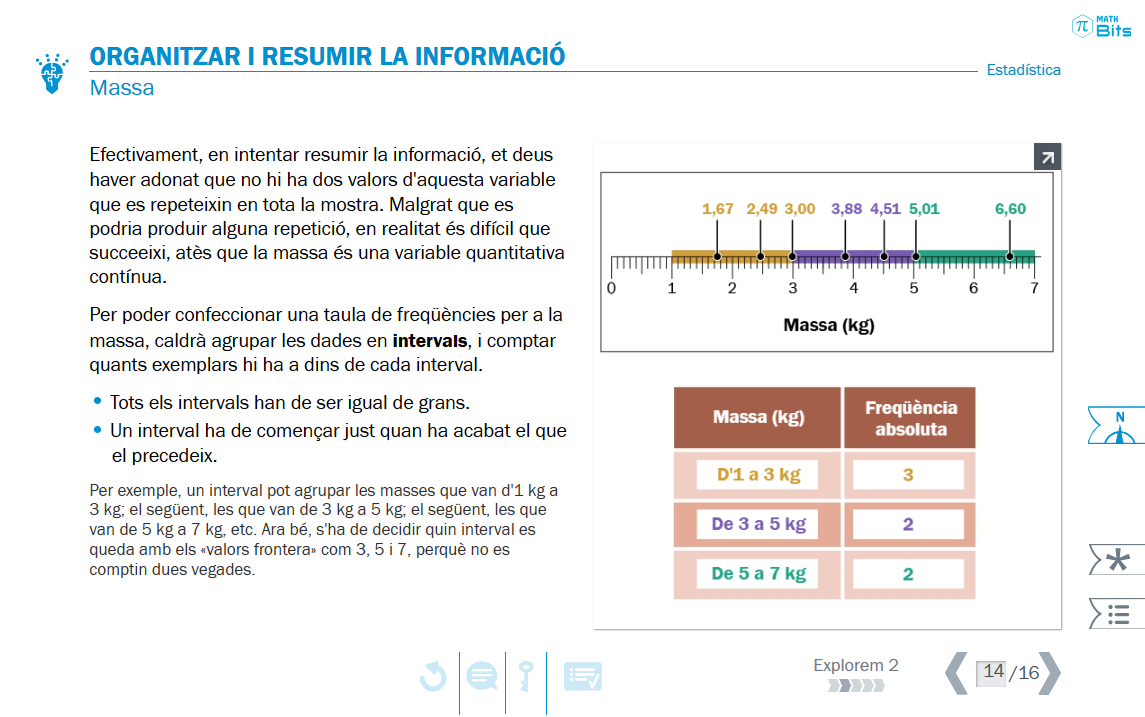
Recurs interactiu que aborda la creació d’intervals per a dades agrupades.

Cada tipus de variable requereix un tipus de gràfic, tot i que en alguns casos existeixen diferents opcions vàlides o adequades. Per exemple, els diagrames de barres es fan servir per representar variables quantitatives discretes o qualitatives, i la seva principal característica és que l’alçària de les barres és proporcional a la freqüència. A més a més, les dades estan ordenades d’esquerra a dreta. Per aquest motiu, són especialment idonis per a variables que es poden ordenar, mentre que els diagrames de sectors resulten més adequats per a variables qualitatives nominals. Malgrat això, els diagrames de sectors es llegeixen molt malament quan el nombre de valors és molt elevat, fet que fa més convenient l’ús de diagrames de barres també en aquests casos.

En qualsevol cas, el més interessant radica en debatre sobre l’adequació d’un tipus de gràfic o un altre i sobre la manera més eficient i precisa de presentar la informació.

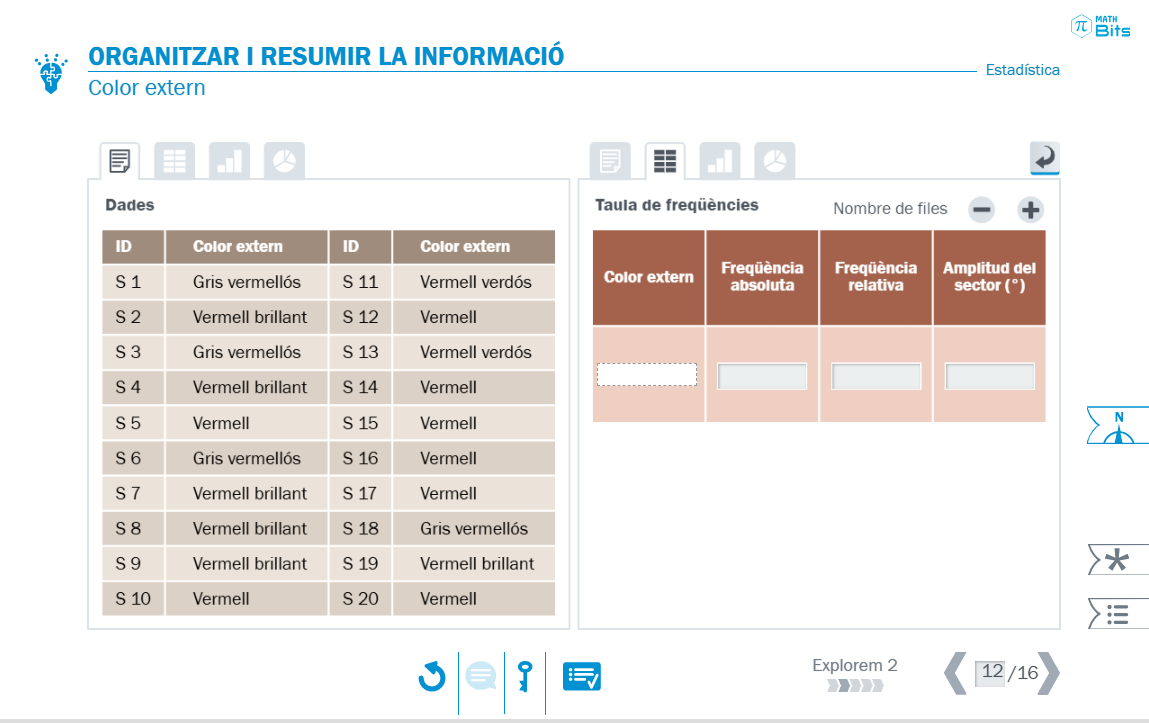
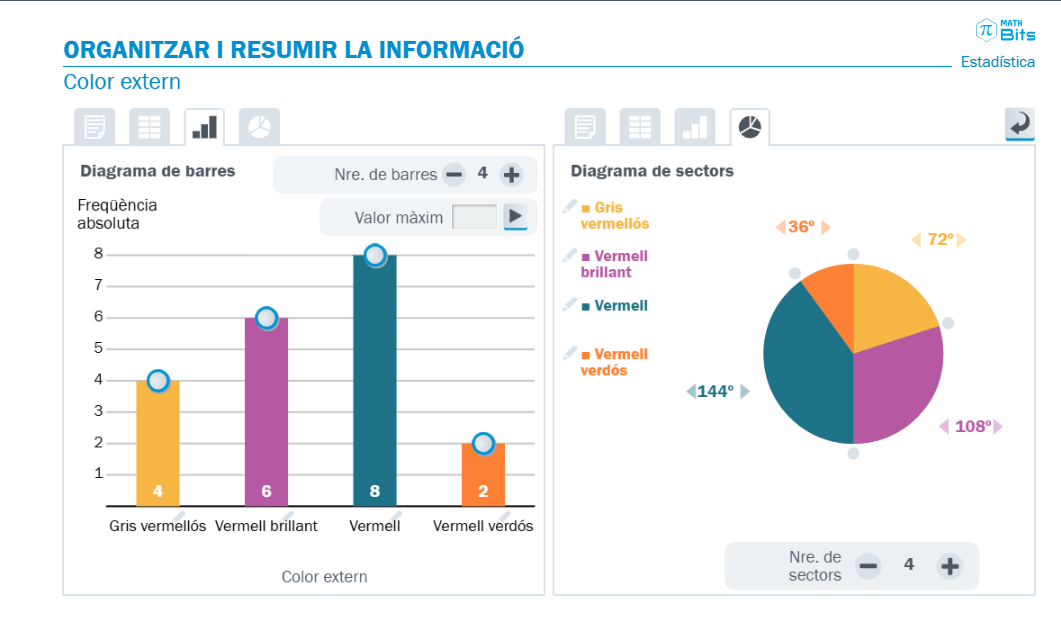
Recursos interactius per construir gràfics estadístics i debatre sobre la seva adequació.

Després d’organitzar i representar el conjunt de les dades, el pas següent és reduir-lo a un únic valor representatiu de tot el conjunt, és a dir, una mesura de tendència central. A la unitat es plantegen activitats per explorar diferents mesures de tendència central, conjuntament amb les seves propietats. Concretament, s’analitza la relació entre la mitjana i la mediana, i es debat en quins contextos resulta més apropiat utilitzar cada una d’elles.

Es plantegen recursos interactius que permeten fer una aproximació intuïtiva a la idea de mediana.

Després d’haver abordat les mesures de centralització, és el torn de les mesures de dispersió. Per això es planteja el problema de distingir quantitativament mostres que comparteixen la mateixa mitjana però que presenten diferències visibles en les dades.

En primer lloc, s’introdueix el rang, que és una mesura de dispersió molt simple, però poc precisa. En analitzar de manera més detallada la distància entre cada una de les dades i la mitjana, s’arriba a la idea de desviació mitjana, que és una mesura de dispersió més precisa.

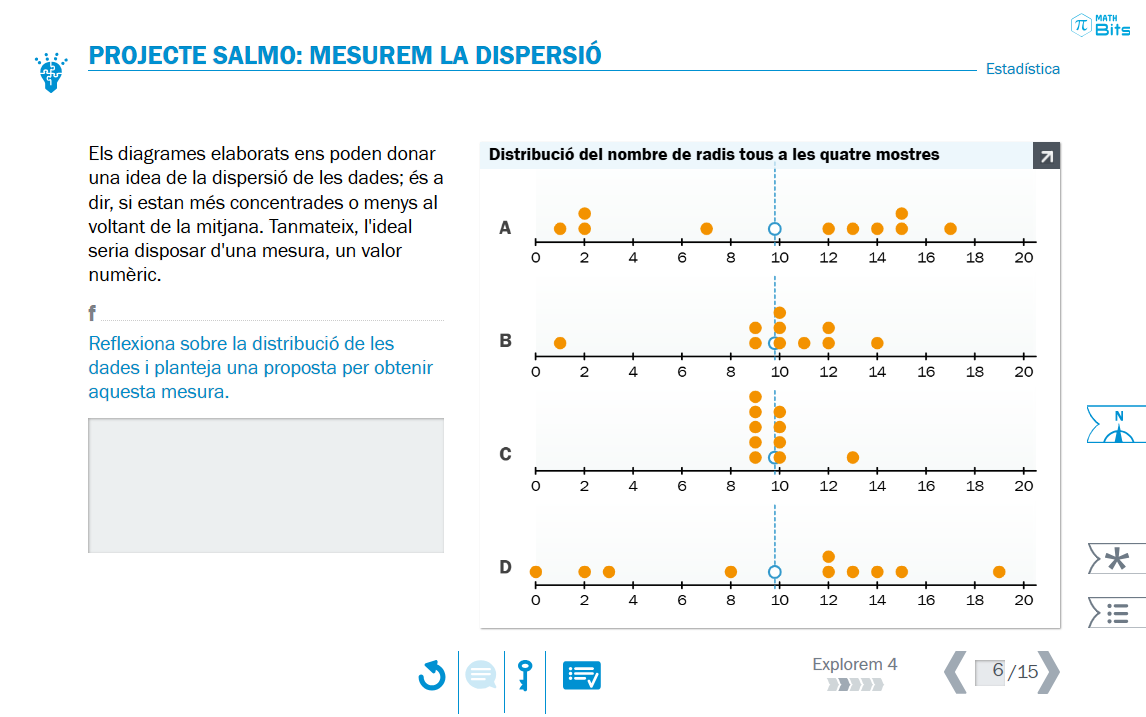
Aproximació visual a la idea de dispersió.

Per acabar la unitat, es planteja una activitat de tipus «Elaborem» on l’alumnat té l’oportunitat d’integrar tot allò que ha après en un projecte complet d’investigació.

Voleu conèixer les propostes didàctiques de Math Bits?

Si esteu interessats a conèixer una proposta pedagògica basada en la investigació i el descobriment guiats, i altament motivadora pels vostres estudiants, poseu-vos en contacte amb nosaltres i us donarem accés a les primeres unitats de mostra.

Referències

Arteaga, P., Batanero, C., Contreras, J. M., y Cañadas, G. (2016). Evaluación de errores en la construcción de gráficos estadísticos elementales por futuros profesores. Revista latinoamericana de investigación en matemática educativa, 19(1), 15-40.

Bargagliotti, A., Franklin, C., Arnold, P., Gould, R., Johnson, S., Perez, L., y Spangler, D. A. (2020). Pre-K-12 guidelines for assessment and instruction in statistics education II (GAISE II) (Second edition). Alexandria, Estats Units: American Statistical Association.

Batanero, C., y Díaz, C. (2011). Estadística con proyectos. Granada, España: Departamento de Didáctica de la Matemática.

Batanero, C., Godino, J., Green, D., Holmes, P., y Vallecillos, A. (1994). Errores y dificultades en la comprensión de los conceptos estadísticos elementales. International Journal of Mathematics Education in Science and Technology, 25(4), 527-547.

Mayén, S., Díaz, C., y Batanero, C. (2009). Conflictos semióticos de estudiantes con el concepto de mediana. Statistics Education Research Journal, 8(2).